CIRCUITOS COMBINACIONALES

DEFINICION:;

Circuito combinacional. Está formado por funciones lógicas elementales ( AND, OR, NAND, NOR, etc. ), que tiene un determinado número de entradas y salidas. Es un circuito cuya salida depende solamente de la «combinación» de sus entradas en el momento que se está realizando la medida en la salida.

Los circuitos de lógica combinacional son hechos a partir de las compuertas básicas compuerta AND, compuerta OR, compuerta NOT. También pueden ser construidos con compuertas NAND, compuertas NOR, compuerta XOR, que son una combinación de las tres compuertas básicas.

TABLA DE VERDAD

DEFINICION:

Tablas de verdad o tabla de valores de verdad, es una tabla que muestra el valor de verdad de una proposición compuesta, para cada combinación de valores de verdad que se pueda asignar a sus componentes.

en la tabla mas se ve sus proposiciones y función de cada una de ellas.

La tabla de los «valores de verdad», es usada en el ámbito de la lógica, para obtener la verdad (V) o falsedad (F), valores de verdad, de una expresión o de una proposición. Además sirven para determinar si es que un determinado esquema de inferencia es formalmente válido como un argumento, llegando a la conclusión de que este es una tautología (se habla de una tautología cuando todos los valores de la tabla mencionada son «V» o sea verdadero

Qué son las tablas de la verdad

Las tablas de verdad son, por una parte, uno de los métodos más sencillos y conocidos de la lógica formal, pero la mismo tiempo también uno de los más poderosos y claros. Entender bien las tablas de verdad es, en gran medida, entender bien a la lógica formal misma.

P	Q	^Q
1	1	1
1	0	0
0	1	0
0	0	0

Fundamentalmente, una tabla de verdad es un dispositivo para demostrar ciertas propiedades lógicas y semánticas de enunciados del lenguaje natural o de fórmulas del lenguaje del cálculo proposicional:

1. . Sin son tautológicas, contradictorias o contingentes
2. . Cuáles son sus condiciones de verdad
3. . Cuál es su rol inferencial, es decir, cuáles son sus conclusiones lógicas y de qué otras proposiciones se siguen lógicamente

• 

FUNCION CANONICA

DEFINICION :

En Álgebra booleana, se conoce como término canónico de una función lógica a todo producto o suma en la cual aparecen todas las variables en su forma directa o inversa. Una Función lógica que está compuesta por operador lógico puede ser expresada en forma canónica usando los conceptos de minterm y maxterm. Todas las funciones lógicas son expresables en forma canónica, tanto como una «suma de minterms» como «producto de maxterms». Esto permite un mejor análisis para la simplificación de dichas funciones, lo que es de gran importancia para la minimización de circuitos digitales.

la función canónica es una forma mas fácil de reducción de dígitos es como una ecuación .

Una función booleana expresada como una disyunción lógica (OR) de minterms es usualmente conocida la «suma de productos«, y su Dual de Morgan es el «producto de sumas«, la cual es una función expresada como una conjunción lógica (AND) de maxterms.

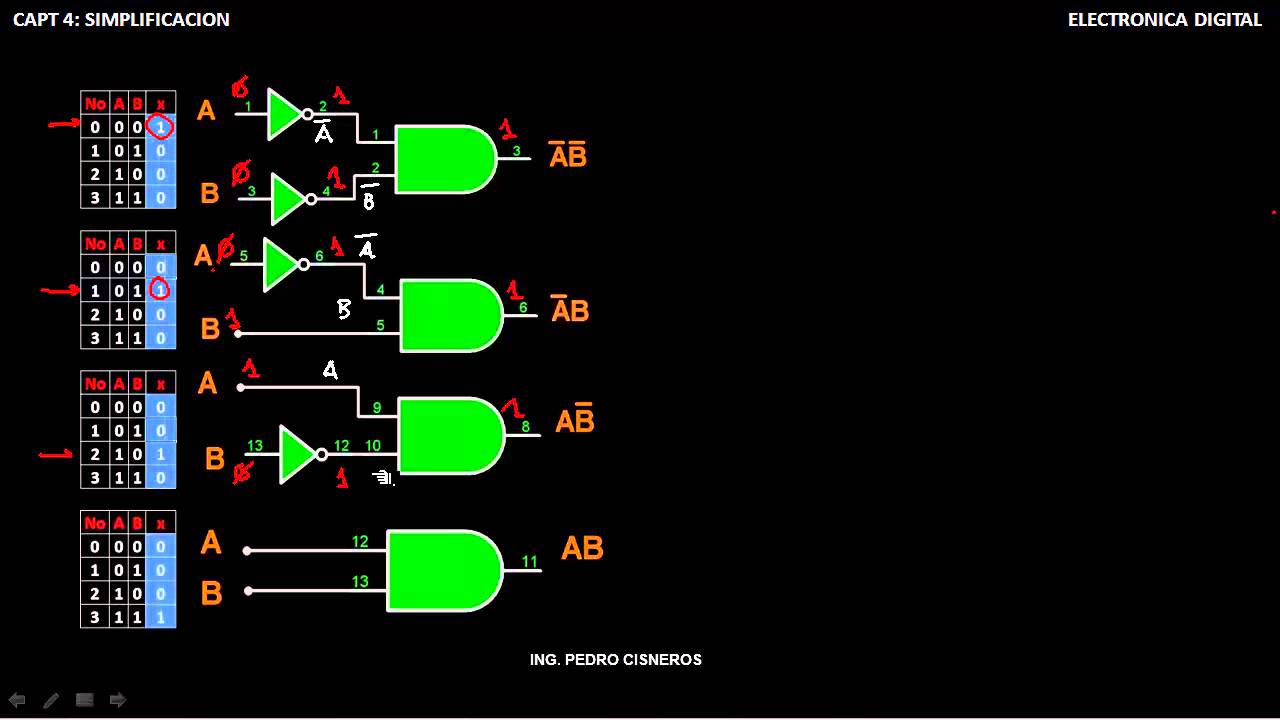
EJERCICO 1

DISEÑO DED CIRCUITO COMBINACIONAL POR SOFWARD CAD

DEFINICION:

7.1. Componentes básicos.
Las componentes digitales electrónicas han evolucionado rápidamente. Se han logrado elevados niveles de integración; es decir gran número de compuertas y flip-flops en un solo dispositivo.

Para manejar el nivel de complejidad, de un proyecto que emplee elevado número de componentes, se han desarrollado herramientas de apoyo al diseño, las cuales también han evolucionado con las nuevas metodologías de diseño de software.

Debido a que los problemas computacionales que deben ser resueltos son de gran complejidad, y a menudo de costo exponencial, se han desarrollado heurísticas y nuevos conceptos para describir sistemas digitales.

En la actualidad los dispositivos integrados se han incrementado y evolucionado con componentes mas complejos y fáciles de utilizar ,tales casos hay como las compuertas .

video de diseño de circuitos combinacionales:

link

tabla Karnaugh

definición:

¿Qué es un Mapa de Karnaugh?

Los Mapas de Karnaugh son una herramienta muy utilizada para la simplificación de circuitos lógicos. Cuando se tiene una función lógica con su tabla de verdad y se desea implementar esa función de la manera más económica posible se utiliza este método.

Ejemplo: Se tiene la siguiente tabla de verdad para tres variables. Se desarrolla la función lógica basada en ella. (primera forma canónica). Ver que en la fórmula se incluyen solamente las variables (A, B, C) cuando F cuando es igual a “1”. Si A en la tabla de verdad es “0” se pone A, si B = “1” se pone B, Si C = “0” se pone C, etc.

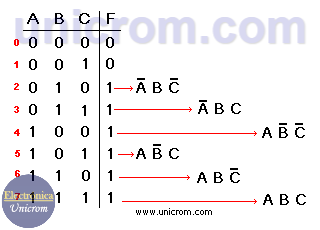
F = A B C + A B C + A B C + A B C + A B C + A B C

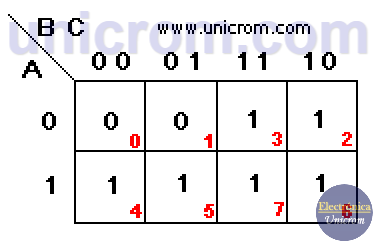
Una vez obtenida la función lógica, se implementa el mapa de Karnaugh. Este tiene 8 casillas que corresponden a 2ⁿ, donde n = 3 (número de variables (A, B, C)). Ver el diagrama arriba. La primera fila corresponde a A = 0 La segunda fila corresponde a A = 1 La primera columna corresponde a BC = 00 (B=0 y C=0).

La segunda columna corresponde a BC = 01 (B=0 y C=1) La tercera columna corresponde a BC = 11 (B=1 y C=1) La cuarta columna corresponde a BC = 10 (B=1 y C=0)

En el mapa de Karnaugh se han puesto “1” en las casillas que corresponden a los valores de F = “1” en la tabla de verdad. Tomar en cuenta la numeración de las filas de la tabla de verdad y la numeración de las casillas en el mapa de Karnaugh.

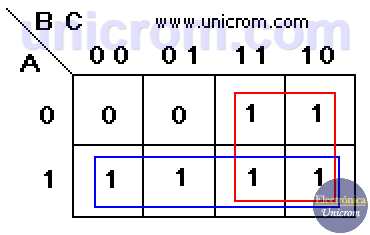
Para proceder con la simplificación, se crean grupos de “1”s que tengan 1, 2, 4, 8, 16, etc. (sólo potencias de 2). Los “1”s deben estar adyacentes (no en diagonal) y mientras más “1”s tenga el grupo, mejor. La función mejor simplificada es aquella que tiene el menor número de grupos con el mayor número de “1”s en cada grupo

Se ve del gráfico que hay dos grupos cada uno de cuatro “1”s, (se permite compartir casillas entre los grupos). La nueva expresión de la función boolena simplificada se deduce del mapa de Karnaugh.

• Para el primer grupo (rojo): la simplificación da B (los “1”s de la tercera y cuarta columna corresponden a B sin negar)
• Para el segundo grupo (azul): la simplificación da A (los “1”s están en la fila inferior que corresponde a A sin negar).

Entonces el resultado es F = B + A  ó   F = A + B

Ejemplo: Una tabla de verdad como la de la derecha da la siguiente función booleana: F = A B C + A B C + A B C + A B C

Se ve claramente que la función es un reflejo del contenido de la tabla de verdad cuando F = “1”, Con esta ecuación se crea el mapa de Karnaugh y se escogen los grupos. Se lograron hacer 3 grupos de dos “1”s cada uno. Se puede ver que no es posible hacer grupos de 3, porque 3 no es potencia de 2. Se observa que hay una casilla que es compartida por los tres grupos.

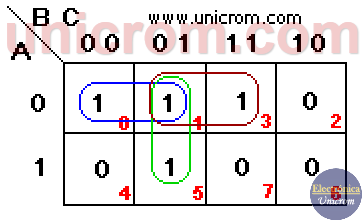
La función simplificada es: F = A B+ A C + B C. Grupo en azul: A B, grupo marrón: A C, grupo verde:B C.

método de mapas para simplificación de algebras booleanas con ese es otro nombre al que se le conoce el mapa de Karnaugh

para implementar el mapa de Karnaugh es muy importante que este presente la tabla de verdad.

link